"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

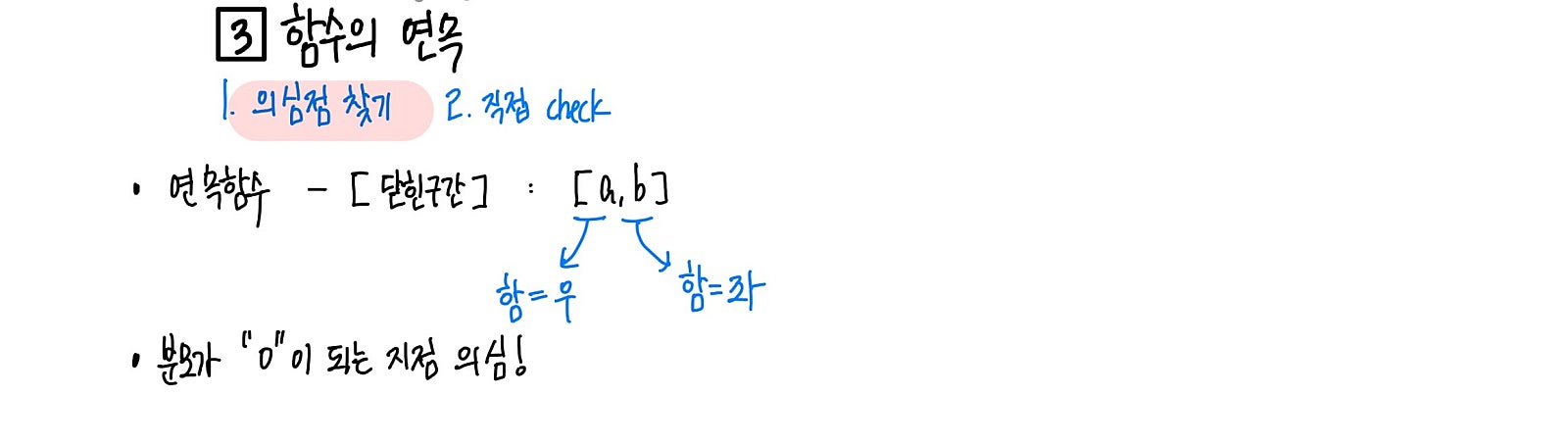
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
8번까지 풀엇는데 11
서술 오류 하나 과조건 하나 찾음 잘 해내고 잇는 듯하다
-
저오늘 생일이에요 27
감사합니다
-
아마 인간이 아닐거야 근데 나 고백받은적 0번인데
-
얘는!
-
윽건이 열받내 20
기벡으로 유명해진거 아니셧습니가 왜 버렷음..
-
심심해서 응원가 써봄 12
진리의 빛이여 조국의 미래여 누가 길을 묻거든 관악을 보게 하라 겨레의 등불이여...
-
현우진 기하 8
ㄹㅇ순수의문인데 왜 우진티는 기하 취급도 안하심? 돈 안되어서…?
-
강사들이 나서서 기트남어라고 조롱하고 유기하니까 학생들도 하면 좃대는 과목이구나...
-
근데 수시 다떨어짐;
-
갑자기 이해가 안되네 적을 이유가 없는데
-
삼반수고민되네 1
~혼자주저리주저리하는글~ 재수해서 연고상경갈거같은데 원래는 설문과나 의류...
-
수시라는 제도는 지금 당장 공부 못하는 학생에게 너무 가혹함 1
정시는 지금 못하더라도 실력을 늘리면 수능에서 우수한 점수를 받을 수 있는데 수시는...
-
내신은 ㅈ빠지게 해도 안올랏음 난.. 수능 언매 만점 독서 1틀 백분위 99인데...
-
대학커뮤니티 노크에서 선발한 성균관대 선배가 오르비에 있는 예비 성균관대학생,...
-
ㅈㄱㄴ
-
이모,이모부에 사촌형누나오는데 공부시간도 없을듯 그리고 아빠몰래 수능준비하는거여서...
-
정시의 최대장점 4
재밌음 수시따위가 비빌 재미가 아님
-
ㅇㅈ끝났나 0
오늘은 삼삼하군
-
레어가져가줘 0
형
-
와 이런 개같은 풀이도 있구나 생각함? 손풀이 보면 계산까지 다들 깔끔하게 풀길래
-
근황 귱금하네
-
내신재탕은 진짜 선넘는다 삼수까지만 내신쓸수잇게해라.
-
결코 다시 전쟁
-
크롬으로 안들어가져서 사파리켬
-
한의사가 뭘로 그렇게 많이 벌었길래 그리 높았음? 한약?
-
이 문제를 통해 2가지의 배울만한 마인드가 있습니다.1) 수능 문제수능 문제는...
-
수끼야아악
-
(가)조건 과조건 아님? oT랑 oA 수직이고 oT 각도pi/6인거도 구해지고...
-
내 방 이쁘지? 17
야광별 스티커붙여서 밤에 이쁨
-
ㅇㅇ....
-
진짜 외로워
-
자지마 3
마!!!!
-
수시로 가면 2
꽃동네 대학 가야해..
-
이새끼들 사회성은 엔수생이랑 비교가안됨
-
400에러뜨던데 나만그랬나
-
볼라벤 하이선 마이삭 힌남노 얘네들도 기억나네
-
예비 19번이면 내려놓고 편히 재수 시작하는게 맞겠죠?
-
정시그만때려요 5
아아 아프다고!!!! 그만패 ㅠㅠ
-
어그로 3
ㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣㅣ 끌렸죠?
-
놀리던 사람들 잘못하면 그 수업 듣게 생겼네 무슨 느낌일까 잘만하면 최지욱쌤처럼...
-
야추 ㅇㅈ 9
-
뽑아놓으면 도망가 사화성떨어져 아웃풋 밀려 그저 수시에서 패했을뿐인 범부
-
메타전환 메타 2
벌써 메타전환이군
-
야ㄷ같이 노골적인 자세의 초딩 알몸 ai 그림 보면 무슨 생각 들 것 같음? 애니...
-
자다 깸 0
다시 재워죠
-
남자 기준!
-
인생이 비참해져요









































